Presentación
El Doctorado en Ciencias con Mención en Matemática tiene como objetivo formar investigadores de excelencia, capacitados para destacar en su área de especialización. Desde la formación inicial, el programa prepara a los estudiantes para desenvolverse con éxito en su campo elegido. Ubicado en la Macro Región Centro Sur Andina, el programa se desarrolla en un entorno de rica diversidad cultural, apoyado por un capital humano altamente calificado y una infraestructura que cumple con las exigencias actuales. Este doctorado, ofrecido por la Universidad de Tarapacá en el Norte Grande de Chile, representa una oportunidad única de formación avanzada en matemáticas. Lejos del centro político y económico del país, el programa se enfoca en abordar la escasez de especialistas en la macro región andina, convirtiéndose en un motor clave para el desarrollo de la disciplina en la región. |

Proceso de postulación cerrado
Fecha de inicio: 25 de agosto de 2025
Fecha de término: 20 de octubre de 2025
El Doctorado en Ciencias con Mención en Matemática cuenta con tres (3) vacantes para la cohorte 2026.
Información
Grado que Otorga
- Doctor/a en Ciencias con Mención en Matemática.
Duración del Programa
- Cuatro años. Ocho semestres académicos. 240 SCT.
Modalidad y horario del Programa
- Presencial. Dedicación exclusiva.
Sede
- Campus Saucache. Av. 18 de septiembre #2222. Arica, Región de Arica y Parinacota.
PLAN DE ESTUDIO
Perfil de graduación
El perfil de la/el graduada(o) del programa de Doctorado en Ciencias con Mención en Matemática se caracteriza por tener los conocimientos, habilidades y aptitudes para formular y desarrollar investigación en Matemática en forma autónoma en el área de su especialización, contribuyendo así al desarrollo científico de la sociedad.
Objetivos del Programa
Objetivo General:
El Programa tiene como objetivo formar Doctores en Ciencias con Mención Matemática, con sólidos conocimientos en la línea de investigación elegida, y capaces de realizar investigación original en forma autónoma y colaborativa, siguiendo los estándares académicos internacionales.
Objetivo Específicos:
- Contribuir al desarrollo nacional y de la Macro Región Centro Sur Andina a través de la formación de personas con altos niveles de excelencia, capaces de crear conocimiento nuevo en el área de la matemática.
- Formar investigadores capaces de integrar grupos de investigación y de transferir nuevos contenidos de la disciplina, contribuyendo a la ampliación del conocimiento en el área de la matemática.
- Desarrollar las habilidades de comunicación de los estudiantes, en el ámbito disciplinar y de investigación, para difundir en la comunidad científica los avances y resultados obtenidos.
Lineas de Investigación
Análisis Matemático Fuzzy e Intervalar En esta línea de investigación se abordan fundamentalmente tópicos relacionados, entre otros, con los siguientes: Análisis multívoco – análisis fuzzy multívoco; teoría de la medida e integración fuzzy; análisis intervalar – análisis intervalarfuzzy; desigualdades integrales fuzzy; optimización fuzzy -optimización intervalar. Ecuaciones Diferenciales Parciales Los principales tópicos de estudio son: la existencia, unicidad, regularidad y estabilidad (comportamiento asintótico) de ecuaciones en derivadas parciales no lineales y de orden alto, tales como Korteweg-de Vries, Beney-Lin, Schrödinger, Navier-Stokes, sistemas micropolares, sistemas de Boussinesq, sistemas de quimiotaxis atractivos y repulsivos. Así como también, el análisis continuo de problemas de control óptimo para sistemas acoplados de ecuaciones diferenciales parciales. Geometría y Teoría de Control La presente área tiene como interés el estudio de problemas matemáticos que contribuyan a la geometría. Los tópicos de estudio son: Teoría geométrica de control, geometría Sub-Riemanniana y áreas afines. Optimización Se estudian los problemas de optimización escalares, vectoriales, multívocos, intervalares y fuzzy. También estudia problemas relacionados como las desigualdades variacionales y problemas de equilibrio. Los tópicos que se estudian para estos problemas son: existencia de soluciones, análisis asintótico, estabilidad, buen planteamiento del problema, soluciones aproximadas, convexidad generalizada, condiciones de optimalidad, problemas regulares y no regulares, problemas no diferenciables, regularizaciones cónicas y sensibilidad, y algoritmos numéricos. |
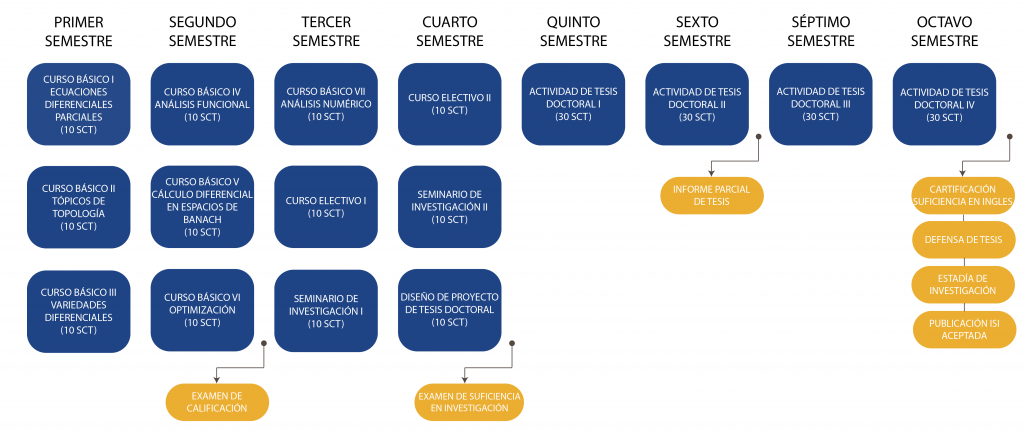
Estructura Curricular
Etapa de Formación Básica Este ciclo contempla un Plan Curricular de tres semestres con un total de siete (7) cursos básicos de formación en matemática y matemática aplicada, pasando por todas las áreas básicas de la matemática como Álgebra, Análisis, Geometría y Topología. Los cursos básicos permiten al estudiante complementar su formación general con conocimientos fundamentales, necesarios para enfrentar la etapa de formación teórica de los cursos electivos y del trabajo de tesis. Además, esta etapa contempla un Examen de Calificación al final del primer año el cual considera los seis (6) primeros cursos básicos. Etapa de formación Avanzada Este proceso de dos semestres de duración contempla dos (2) cursos electivos y dos (2) seminarios de investigación, seguidos de un Diseño del Proyecto de tesis Doctoral. Mediante los cursos electivos, el estudiante comenzará su formación teórica en la línea de investigación en la cual desea desarrollar su trabajo de tesis. En los seminarios de investigación, el estudiante se familiarizará con las líneas de investigación del programa mediante la lectura y presentación de artículos de investigación. El Diseño del proyecto de Tesis Doctoral es redactado por el estudiante en conjunto con un/a Director/a de tesis que es un académico miembro del Claustro, experto en una de las líneas de investigación del Programa. La defensa del Proyecto de Tesis Doctoral se realiza ante una Comisión nombrada por el CAP. En dicha defensa, el/la estudiante evidenciará su suficiencia investigativa, ciclo que exige un régimen semipresencial. Etapa de Investigación Este proceso contempla de cuatro (4) actividades de Tesis Doctoral, un (1) informe parcial de Tesis al finalizar el tercer año y de una estadía de investigación. En las cuatro (4) actividades de Tesis Doctoral, el/la estudiante realizará el trabajo de tesis bajo la tutela de el/la Director/a de Tesis. Se realizará una investigación planificada en su proyecto de tesis. El/la Director/a de Tesis llevará control del trabajo de tesis en una bitácora de trabajo donde se indicará las fechas de trabajo con el estudiante y las actividades realizadas en dichas fechas. El/la Director de Tesis podrá pedir al estudiante que tome algún curso electivo si lo considera necesario para el desarrollo de la tesis Doctoral. Asimismo, durante el tercer o cuarto año, el/la Director/a de Tesis gestionará que el/la estudiante realice una estadía de investigación en una Universidad o Centro de Investigación nacional o extranjero. Al finalizar la estadía, el/la estudiante deberá presentar un informe escrito de las actividades realizadas durante su estadía. Además de las asignaturas y actividades mostradas en la malla curricular, los estudiantes deberán completar las siguientes actividades obligatorias:
|
Cuerpo
Académico
PROFESORES DE CLAUSTRO











PROFESORES COLABORADORES


ADMISIÓN
Requisitos de Ingreso
Para postular al Programa de Doctorado, los candidatos deben cumplir con los siguientes requisitos mínimos:
|
Documentos para postulación
- Certificado de grado de Licenciado en Matemática o equivalente.
- Certificado del grado de Magíster en Matemática o equivalente.
- Certificado de nacimiento.
- Certificado de concentración de notas de Pregrado conducente al grado de Licenciatura en Matemática o equivalente.
- Certificado de concentración de notas del Magíster
- Documento de identidad vigente válido en territorio nacional. (C.I, Pasaporte o DNI)
- Carta de recomendación de dos académicos/as nacionales o extranjeros/as en el ámbito de la Matemática. Las cartas deben ser enviadas directamente por el/la recomendante al correo del programa.
- Resumen de antecedentes que muestre su experiencia en docencia, investigación o trabajo en la disciplina, expresada mediante la dictación de cursos, en la participación en proyectos concursables, publicaciones, asistencia a escuelas, congreso, etc. y en general mostrando su trayectoria académica o profesional.
- Carta de intención breve donde se indique la línea de investigación de su interés y las razones que fundamenten su postulación al programa (máximo 2 página)
Sistema de Selección
Todos(as) los(as) postulantes deben rendir un examen escrito aprobado por el CAP. Una vez que se tengan los resultados de este examen, el CAP analizará todos los antecedentes presentados por cada postulante, elaborando un ranking de todos(as) los(as) postulantes. Para elaborar el ranking, se tomará en cuenta lo siguiente:

Para postular al Programa de Doctorado, los candidatos deben cumplir con los siguientes requisitos mínimos:
|
Beneficios institucionales
El Programa cuenta con tres (3) Becas de Manutención y Arancel Básico y Diferenciado, definidas de la siguiente manera:
|
Contacto
Director del Programa de Doctorado en Ciencias con Mención en Matemática
- Dr. Yurilev Chalco Cano
- ychalco@academicos.uta.cl
- (+56) 58 2 205821
- Avda. 18 de Septiembre # 2222, Campus Saucache. Departamento de Matemática, Segundo piso, oficina 13.
Profesional de Apoyo Doctorado en Ciencias con Mención en Matemática
- Srta. Heleni Galleguillos Carter
- postgradoenmatematica@gestion.uta.cl
- (+56) 582205754
- Avda. 18 de Septiembre # 2222, Campus Saucache. Departamento de Matemática, primer piso, oficina 2.